愿闻其详

随心所写，姑妄听之

0%

图论

发表于 更新于

图

图论基础

  1. 图的同构

    假设 G=(V,E) 和 G1=(V1，E1) 是两个图，如果存在一个双射 m：V→V1 ，使得对所有的x,y∈V 均有 x,y∈E 等价于 m(x) m(y)∈E1 ，则称 G和 G1是同构的。当 G 同构带 G1后，这些顶点可能标号变了，但是如果在“旧”的图中有的关系，在“新”图中依然保留，只不过是“位置”变了。

    图同构问题一般可以分为四个不同的研究种类：精确图完全同构、精确子图同构、不精确图完全同构、不精确子图同构。证明已后面三者是NP-Complete问题，第一类问题还没有定论，一般认为是NP问题。这里讨论的是精确图完全同构。图必须满足以下条件：

    • 节点个数相等

    • 边数相等

    • 对应节点的度相等（包括进度和出度）

    • 节点对应的关系相同（包括重边和环）

    • 在权值图内，各边的权值和对应的关系相同

  2. 如何判断图的同构

    我们可以从满足的条件来看首先可以从最简单，肉眼可见的顶点数开始看。如果G与G2同构，他们的阶和度必须完全相等，如果阶和度不相等就可以直接否定。其次，观察G和G2的双射关系，E(u, v) 需要等价于E1(u1, v1)。如果满足即可推断出两图重构

  3. 图同构的搜索剪枝

    我们可以使用DFS直接对图的双射关系和边，度数进行搜索（将双射映射为u->v的关系)，从而判断是否同构。但是，这样显然会出现大量的重复。我们可以在搜索前进行预处理,将图的边数和度数进行排序 (图的重构与判断双射顺序无关)，先从大的进行遍历。在大度数的情况下，更容易出现不符合的情况，直接返回这种情况，可以有效避免大量无效搜索。

图的储存：

    1. 邻接矩阵

        邻接矩阵是最简单的储存方法，这里就不给代码实现了

        优点：可以O（1）的复杂程度查询边权值

        缺点：占用大量空间，无法存储稀疏图

  1. 邻接表（由于STL存在vector，故此处使用vector替代指针）

    优点：适用于存储较多点数情况，且易于排序

    缺点：无法快速查询边

    代码实现：

    构造

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int n, m;
    vector<vector<int>> adj;  // 图，int可改成node

    int main() {
      cin >> n >> m;
      adj.resize(n + 1);

      for (int i = 1; i <= m; ++i) {
        int u, v;
        cin >> u >> v;
        adj[u].push_back(v);
      }

      return 0;
    }

    查找：

    1
    2
    3
    4
    5
    6
    7
    bool find_node(int u, int v)
    {
     for (int i = 0; i < mp[u].size(); i++) // 注意从0开始
     if (mp[u][i].v == v) // 遍历这个点的所有出度
     return true; 
    return false;
    }

    dfs:

1
2
3
4
5
6
7
8
9
10
vector<bool> visit;

void dfs(int u)
{
    if (visit[u]) return;
    visit[u] = true;

    for (int i = 0; i < mp[u].size(); i++)
        dfs(mp[u][i].v);
}
  1. 链式前向星优点：易用于网络流缺点：无法快速查询边，配套代码麻烦
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    void add(int u, int v) {
      nxt[++cnt] = head[u];  // 当前边的后继
      head[u] = cnt;         // 起点 u 的第一条边
      to[cnt] = v;           // 当前边的终点
    }

    // 遍历 u 的出边
    for (int i = head[u]; ~i; i = nxt[i]) {  // ~i 表示 i != -1
      int v = to[i];
    }

最短路径：

  1. Dijsktra

     传统地使用数组暴力维护Dijsktra算法会导致时间复杂度达到O（n^2 + m) ,可视作O（n^2)，显然这种代价过高，我们可以使用优先队列来维护。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct edge
{
 int d;   // 目的节点
 int w;  // 
};

struct djNode
{
 int u;
 int pre;
 int nowDis;
};


vector<

树

二叉树

  1. 常见的三种遍历

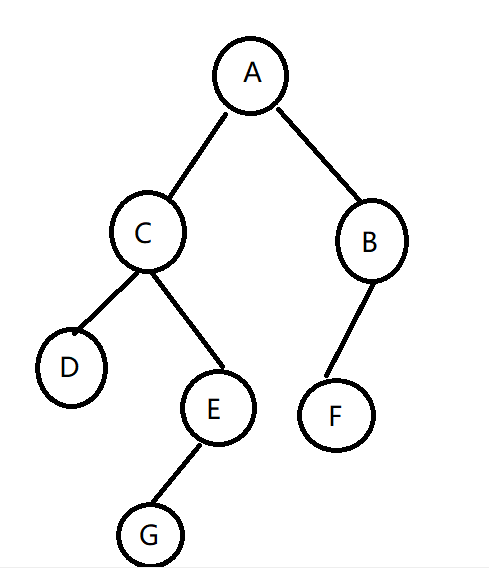
    常规二叉树有三种遍历方式，先序，中序和后序遍历。先序遍历是按头，左（子树），右（子树）的方式遍历，中序遍历是按左，头，右的方式遍历，后序遍历是按左，右，头的顺序遍历。

    按图上来说，先序遍历是ACDEGBF, 中序遍历是DCGEAFB，后序遍历DGECFBA。

  2. 根据遍历建树

    一般来说，必须给中序遍历才能建树。

    宏定义

1
2
3
4
5
6
7
8
9
#define SPTR   // 宏开关，如果在竞赛中释放时间过大，删去开关加速
#ifdef SPTR
template <class T>
using sptr = shared_ptr<T>;
#endif
#ifndef SPTR
template <class T>
using sptr = T*;
#endif

前序，中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int n;
vector<int> preOrder;
vector<int> inOrder;

sptr<nodeTree> build(int il, int ir, int pl, int pr)   // 递归建树
{
    if (il > ir) return nullptr;
    if (pl > pr) return nullptr;

    sptr<nodeTree> root (new nodeTree(preOrder[pl]));
    int i = il;
    while (inOrder[i] != preOrder[pl]) i++;
    int cnt = i - il;

    root->left = build(il, i - 1, pl + 1, pl + cnt);
    root->right = build(i + 1, ir, pl + cnt + 1, pr);
    return root;
}

  中序，后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int n;
vector<int> postOrder;
vector<int> inOrder;

sptr<nodeTree> build(int il, int ir, int pl, int pr)
{
    if (il > ir) return nullptr;
    if (pl > pr) return nullptr;

    sptr<nodeTree> root(new nodeTree(postOder[pr]));
    int i = il;
    while (inOder[i] == postOder[pr]) i++;
    int cnt = i - il;

    root->left = build(il, i - 1, pl, pl + cnt - 1);
    root->right = build(i + 1, ir, pl+cnt, pr - 1);
    return root;
}